The Upcoming Tezos Jakarta Protocol will support compact Merkle proofs to scale the network's trust infrastructure. This allows nodes that do not trust each other to agree on the validity of Tezos transactions with orders of magnitude smaller storage requirements. For instance, the block 2,400,319, containing 402 transactions and 638 operations, can be validated using a Merkle proof of 6.3 MB instead of requiring a Tezos node with at least 3.4 GB of storage, a savings of 99.8%!

Tarides contributed to Jakarta by extending the Tezos storage system to support compact storage proofs. This feature extends the compact cryptographic representation of the ledger state to sequences of operations. As a result, nodes that do not trust each other can still agree on the series of operations' validity, even if they don't know the entire contents of the ledger. The upcoming stateless nodes (like Tezos light-client), proxies, and mechanisms that allow the exchange of trust between disjointed tamper-proof storage (like L2 transactional-rollups, L2 smart-contract rollups,...) will use these proofs to scale the Tezos trust infrastructure to new heights.

The Merkle Proof API is one of the last major features that we integrated from Plebeia. It is the result of a years-long collaboration between DaiLambda and Tarides to improve the storage system of Tezos.

A (Very) Quick Tour of Tezos

The Tezos network builds trust between its nodes by using two components:

• (i) a tamper-proof database that can generate cryptographic hashes, which uniquely and compactly represent the state of its contents; and
• (ii) a consensus algorithm to share these cryptographic hashes across the network of (potentially adversarial) nodes.

Both components have seen impressive improved performance recently. First, for (i), we've discussed the improvements that we released in Octez v13 to improve the efficiency of the storage component by a factor of 6. Second, for (ii), the consensus algorithm in Ithaca 2 changed from a Nakamoto-style algorithm (like Bitcoin) to Tenderbake -- a Byzantine Fault Tolerance consensus with deterministic finality. This change significantly improved the time it takes for converging towards a uniquely agreeing state hash in the Tezos network.

The Merkle proofs that we introduced in the Jakarta Protocol will allow us to improve the chain's performance even more.

The Tezos Ledger is a Merkle Tree

Tezos represents the ledger state (for instance, the amount of tokens owned by everyone) as a Merkle tree, using the Irmin storage library. Merkle trees are immutable tree-like data structures where each leaf is labelled with a cryptographic hash. Each node's hash is then obtained by recursively hashing its children's label. Tezos then combines that root hash computation with its consensus protocol to make sure every node in the network agrees on the ledger's state.

But there is another interesting aspect of Merkle trees that was not exposed and used by Tezos until now: Merkle proofs. In the protocol J proposal, we are introducing a new feature: Merkle proofs for Tezos as partial, compressed, Merkle trees. In a blockchain, as in Tezos, Merkle proofs are an efficient way to verify the integrity of operations over Merkle trees. For this reason, Merkle proofs are a central part of the optimistic rollups projects that will be available with the Tezos Jakarta Protocol.

In collaboration with DaiLambda, Marigold, Nomadic Labs, and TriliTech, we have integrated Plebeia Merkle proofs in Irmin. Plebeia use Patricia binary trees that are capable of generating very compact Merkle proofs. For instance, the proof of 100 operations can be represented within 46 kB, while storing the full Tezos context requires 3.4 GB of disk storage to store the relevant context. This compactness comes from its specialised store structure and clever optimisations, such as path compression and inlining. We have been working with the DaiLambda team to unite Irmin and Plebeia's strengths and bring built-in compact Merkle proof support to Tezos. We added support for both the existing storage stack, where trees have a branching factor of 32, and for new L2 storage systems that could use binary trees directly. We have also worked with Marigold and Nomadic Labs to propose an alternative representation of these proofs using streams, that comes with a simplified verification algorithm. A stream proof encodes the same information as a regular proof. However, instead of being encoded as a tree, the proof is encoded as a sequence of steps that reveal a Merkle tree lazily, from root to leaves.

Kind of Proofs	1 op.	100 ops.	1k ops.	10k ops.
binary Merkle trees	0.7kB	46kB	371kB	2.8MB
stream binary Merkle trees	1kB	75kB	602kB	4.5MB
Merkle B-trees (32 children)	3.1kB	158kB	1232kB	7.8MB
stream Merkle B-trees (32 children)	3.1kB	158kB	1238kB	7.9MB

The table above shows the size for such proofs, using 2.5M entries (the current number of entries in /data/contracts/index in the Tezos context). We are simulating 1, 100, 1000, and 10_000 random read operations on the entries, and we display the size of the related proofs.

An Example

Let's look at a simple example of a Merkle proof produced for ensuring tamper-proof banking account statements.

We can model a bank that stores its customer balances in the form of a Merkle tree. To avoid publishing the entire contents of its customer accounts, this bank can publicly export the bank's Merkle tree's hash. To let 3rd-parties validate an operation, it can also produce Merkle proofs that reveal the balance of some customers. Anyone in possession of a Merkle proof can hash it and verify that it hashes identically to the public hash announced by the bank. This equality of hash is proof of correctness.

Our bank contains the balances for Eve (30 coins), Ben (10 coins), and Bob (20 coins). It stores the customers in a radix tree (Eve's balance is stored under "e", "v", "e").

Irmin stores data as hash trees: whenever data is added to the database, the corresponding nodes in the tree are hashed in order to then generate the hash of the root node. The hash of a commit also acts as a reference for accessing it in the future. This storage format is close to Merkle proofs. It suffices to blind the part of the tree that a transaction has not accessed to generate its proof. For example, the account statement for Eve is in green. It doesn't leak sensitive information about the other customers: only the letter "b" is leaked. The hash corresponds to Bob and Ben's subtree.

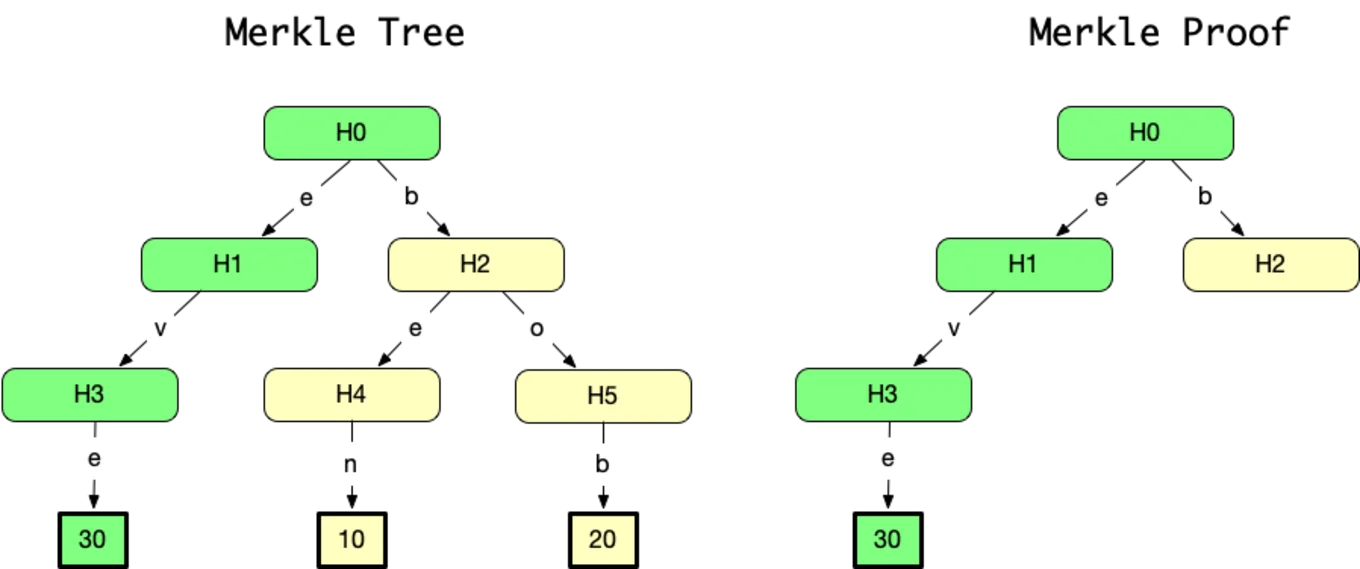
The Figure shows the difference between a Merkle tree (on the left) and a Merkle proof (on the right). In Merkle proofs, some subtrees can be blinded and represented only by their hash. Here the subtree under H2 is blinded and replaced by its hash. Thanks to this, Merkle trees and Merkle proofs will have the same root hash. Merkle proofs are hence very useful to provide Merkle tree summaries for a subset of the full data available.

Merkle proofs are thus partial Merkle trees, with the same root hash. But proofs can also be represented using an alternate definition: a stream of elements that needs to be visited in order to build the tree's root hash. There is a one-to-one correspondence between the two representations, but stream proofs are easier to implement as they encode the order in which nodes have to be visited to verify the proof. However, stream proofs need to carry the hash of all the intermediate nodes, while tree proofs can omit those. As a consequence, tree proofs are smaller than stream proofs, as shown in the above table.

For instance, in the above Figure, the equivalent stream proof is the sequence:

• A leaf with 30 coins;
• A node with hash H3 with a child ("e", "30 coins");
• A node with hash H1 with a child ("v", H3);
• A node with hash H0 with two children ("e", H1) and ("b", H2).

A verifier can just apply these elements in sequence to verify that H0 is a valid root hash.

Merkle Proofs in Irmin

If you want more details about the Merkle proof implementation, head over to the documentation or at https://github.com/mirage/irmin/pull/1802 for the example above revisited in Irmin.